Disclaimer:- All the Information provided in this post are prepared & compiled by A. Praveen Kumar, SPM, Papannapet SO-502303, Telangana State for in good faith of Postal Assistant Exam Aspirants. Author of blog does not accepts any responsibility in relation to the accuracy, completeness, usefulness or otherwise, of contents.
TIME AND DISTANCE
- Speed, Time and Distance:
Speed =
|
Distance
|
,
|
Time =
|
Distance
|
,
|
Distance = (Speed x Time).
| ||||
Time
|
Speed
|
- km/hr to m/sec conversion:
x km/hr =
|
x x
|
5
|
m/sec.
| ||
18
|
- m/sec to km/hr conversion:
x m/sec =
|
x x
|
18
|
km/hr.
| ||
5
|
- If the ratio of the speeds of A and B is a : b, then the ratio of the
the times taken by then to cover the same distance is
|
1
|
:
|
1
|
or b : a.
|
a
|
b
|
- Suppose a man covers a certain distance at x km/hr and an equal distance at ykm/hr. Then,
the average speed during the whole journey is
|
2xy
|
km/hr.
| ||
x + y
|
You have to know only two conversions when needed
1) kilometre/hour into metre/sec use 5/18 from (1000/3600)
2) metre/sec into kilometre/hour use 18/5 from (3600/1000)
Fastest multiplication and division knowledge will help you to solve time and distance easily
For example;
1.A person crosses a 50 m long street in 5sec. What is his speed in km per hour?
Here we came to know he tooks 5 sec to cross 50 metre long
So, he goes 10 metre per second, here use our conversion (2)
10*18/5
2*18=36
That person crosses in the speed of 36 km/hr
|
TIME AND DISTANCE SHORTCUTS
1.If a person travels half a distance in a journey at x km/hr and remaining half at the speed of y km/hr, the average speed of the whole journey is given by:
Example 1
A person travels half of journey at the speed of 30 km/hr and the next half at a speed of 15 km/hr. What is the average speed of the person during the whole journey?
Sol:
Here; x= 30 and y= 15
Putting the values we get:
Answer= 20 km/hr
Short Cut 2
If a person travels three equal distances in a journey at a speed of x km/hr, y km/hr and z km/hr. The average speed is given by:
Example 2
Ravi starts from Delhi to Agra a distance of about 300 kms. He divided his journey into a distance of thee equal parts in terms of distance and covered them with the speed of 30 km/hr, 60 km/hr and 90 km/hr, calculate his average speed during the journey:
Sol:
Here: x= 30, y= 60, z= 90.
Putting the values we get:
Answer= 49.09 km/hr
Short Cut-3
If a person travels Mth part of a distance at x km/hr, Nth part at y km/hr and the remaining Pth part at z km/hr,
Then his average speed in km/hr is given by:
If instead of proportion, the parts of the distance are given in percentage i.e. M%, N% and P% respectively, then the formula becomes:
Example 3
Hari travels 20% of a distance at an average speed of 20 km/hr, next 30% distance at an average speed of 30 km/hr and the remaining 50% of distance at the average speed of 50 km/hr. Find his average speed during the whole journey.
Sol:
Here M=20, N=30 and P= 50 also x= 20, y= 30 and z= 50
Putting the values we get:
Answer =33.33 km/hr
4If a car does a journey in 'T' hrs, the first half at 'a' km/hr and the second half at 'b' km/hr. The total distance covered by the car:
(2 x Time x a x b ) / (a + b).
A motorcar does a journey in 10 hrs, the first half at 21 kmph and the second half at 24 kmph. Find the distance?Sol: Distance = (2 x 10 x 21 x 24) / (21+24)
= 10080 / 45
= 224 km.
5.If a person goes from 'A' to 'B' at a speed of 'a' kmph and returns at a speed of 'b' kmph and takes 'T' hours in all, then the distance between the A and B:
= 10080 / 45
= 224 km.
5.If a person goes from 'A' to 'B' at a speed of 'a' kmph and returns at a speed of 'b' kmph and takes 'T' hours in all, then the distance between the A and B:
Total time taken x (Product of the two Speeds / Addition of the two speeds)
A boy goes to school at a speed of 3 kmph and returns to the village at a speed of 2 kmph. If he takes 5 hrs in all, what is the distance between the village and the school?
Sol: Let the required distance be x km.
Then time taken during the first journey = x/3 hr.
and time taken during the second journey = x/2 hr.
x/3 + x/2 = 5 => (2x + 3x) / 6 = 5
=> 5x = 30.
=> x = 6
required distance = 6 km.
EXAMPLES
1.An athlete runs 200 meters race in 24 seconds. His speed is:
Sol:
|
Speed =
|
|
m/sec =
|
|
m/sec =
|
|
x
|
|
km/hr = 30 km/hr.
|
2.Two trains starting at the same time from two stations 200 km apart and going in opposite directions cross each other at a distance of 110 km from one of the stations. What is the ratio of their speeds?
Sol:
| ||
In the same time, they cover 110 km and 90 km respectively.
| ||
| ||
3.How long will a boy take to run round a square field of side 35 meters, If he runs at the rate of 9 km/hr?
Sol:
| |||||||||||||||
| |||||||||||||||
Distance = (35 x 4) m = 140 m.
| |||||||||||||||
| |||||||||||||||
4.The distance between two cities A and B is 330 km. A train starts from A at 8 a.m. and travels towards B at 60 km/hr. Another train starts from B at 9 a.m. and travels towards A at 75 km/hr. At what time do they meet
Sol:
| |||||
Suppose they meet x hrs after 8 a.m. Then,
| |||||
(Distance moved by first in x hrs) + [Distance moved by second in (x-1) hrs] = 330
| |||||
| |||||
So, they meet at (8 + 3), i.e. 11 a.m.
|
5.A person crosses a 600 m long street in 5 minutes, What is his speed in km per hour
Sol:
|
6.Two men start together to walk to a certain destination, one at 3 kmph and together at 3.75 kmph. The latter arrives half an hour before the former. The distance is:
Sol: Let the distance be x km. Then,
| |||||||||||||||||||||||||
|
7.The ratio between the speeds of two trains is 7: 8. If the second train runs 400 kms in 4 hours, then the speed of the first train is:
Sol: Let the speeds of two trains be 7X and 8X km/hr.
| |||||||||||||||||||
| |||||||||||||||||||
|
8.A is twice as fast as B and B is thrice as fast as C is. The journey covered by C in 54 minutes will be covered by B in:
Sol: Let C's speed = x km/hr, Then, B's speed = 3x km/hr and A's speed = 6x km/hr
| ||||||||||||||
| ||||||||||||||
| ||||||||||||||
If C takes 6 min., then B takes 2 min.
| ||||||||||||||
|
9.A boy rides his bicycle 10 km at an average speed of 12 km/hr and again travels 12 km at an average speed of 10 km/hr. His average speed for the entire trip is approximately
Sol:
| ||||||||||||||||
Total distance travelled = (10 + 12) km/hr = 22 km/hr
| ||||||||||||||||
| ||||||||||||||||
| ||||||||||||||||
10. If a train runs at 40 kmph, it reaches its destination late by 11 minutes but if it runs at 50 kmph, it is late by 5 minutes only. The correct time for the train to complete its journey is:
Sol:
| ||||||||||||||
Let the correct time to complete the journey be x min.
| ||||||||||||||
Distance covered in (x + 11) min. at 40 kmph = Distance covered in (x + 5) min. at 50 kmph
| ||||||||||||||
| ||||||||||||||
11. An express train traveled at an average speed of 100km/hr, stopping for minutes after every 75 km. How long did it take to reach its destination 600 km from the starting point?
Sol:
| |||||||||||
| |||||||||||
| |||||||||||
Total time of stoppage = (3 x 7) min = 21 min.
| |||||||||||
Hence, total time taken = 6 hrs 21 min.
| |||||||||||
12.
Excluding stoppages, the speed of a bus is 54 kmph and including stoppages, it is 45 kmph. For how many minutes does the bus stop per hour?
Sol:
| ||||||||
Due to stoppages, it covers 9 km less.
| ||||||||
|
13.Three persons are walking from a place A to another place B. Their speeds are in the ratio of 4 : 3 : 5. The time ratio to reach B by these persons will be :
Sol: Ratio of speeds = 4 : 3 : 5
| |||||||||||||||
|
14. Walking ¾ of his speed, a person is 10 min late to his office. Find his usual time to cover the distance?
Sol: Usual time = Late time / {1/ (3/4) - 1)
= 10 / (4/3 -1)
= 10 / (1/3)
= 30 minutes.
= 10 / (4/3 -1)
= 10 / (1/3)
= 30 minutes.
15. Running 4/3 of his usual speed, a person improves his timing by 10 minutes. Find his usual timing by 10 minutes. Find his usual time to cover the distance?
Sol: Usual time = Improved time / {1 - (1/ (3/4)}
= 10 / { 1- (3/4) }
= 40 minutes.
16. A train travelling 25 kmph leaves Delhi at 9 a.m. and another train travelling 35 kmph starts at 2 p.m. in the same direction. How many km from will they be together?
= 10 / { 1- (3/4) }
= 40 minutes.
16. A train travelling 25 kmph leaves Delhi at 9 a.m. and another train travelling 35 kmph starts at 2 p.m. in the same direction. How many km from will they be together?
Sol: Meeting point's distance from the starting point = [25 x 35 x (2p.m. - 9 a.m)] / (35 -25)
= (25 x 35x 5) / 10
= 4375 / 10
= 437.5 km .
= (25 x 35x 5) / 10
= 4375 / 10
= 437.5 km .
17. A motor car starts with the speed of 70 km/hr with its speed increasing every two hours by 10 kmph. In how many hours will it cover 345 kms?
Sol:
| |||||||||||||||||
Distance covered in first 2 hours = (70 x 2) km = 140 km
| |||||||||||||||||
Distance covered in next 2 hours = (80 x 2) km = 160 km
| |||||||||||||||||
Remaining distance = 345 – (140 + 160) = 45 km.
| |||||||||||||||||
Speed in the fifth hour = 90 km/hr
| |||||||||||||||||
| |||||||||||||||||
| |||||||||||||||||
18.A person travels from P to Q at a speed of 40 kmph and returns by increasing his speed by 50%. What is his average speed for the both the trips?
Sol:
| ||||||||||||||||
Speed on return trip = 150% of 40 = 60 kmph.
| ||||||||||||||||
|
19.A man takes 5 hours 45 min. in walking to a certain place and riding back. He would have gained 2 hours by riding both ways. The time he would take to walk both ways, is:
Sol:
| |||||||||||||||||||
Let the distance be x km. Then,
| |||||||||||||||||||
| |||||||||||||||||||
| |||||||||||||||||||
| |||||||||||||||||||
| |||||||||||||||||||
20. A can complete a journey in 19 hours. He travels first half of the journey at the rate of 21 km/hr and second half at the rate of 24 km/hr. Find the total journey in km.
Sol: Let the total distance be X km. Then,
| ||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||
21.A man in a train notices that he can count 21 telephone posts in one minute. If they are known to be 50 meters apart, then at what speed is the train travelling?
Sol: Number of gaps between 21 telephone posts = 20
| |||||
Distance traveled in 1 minute = (50 x 20) m = 1000 m = 1 km
| |||||
| |||||
22. Mary jogs 9 km at speed of 6 km per hour. At what speed would she need to jog during the next 1.5 hours to have an average of 9 km per hour for the entire jogging session?
Sol: Let speed of jogging be x km/hr
| |||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||
Total distance covered = (9 + 1.5x) km
| |||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||
23. A train covers a distance of 10 km in 12 minutes. If its speed is decreased by 5 km / hr, the time taken by it to cover the same distance will be:
Sol:
| ||||||||||||||||||||||
| ||||||||||||||||||||||
New speed = (50 – 5) km / hr = 45 km / hr
| ||||||||||||||||||||||
| ||||||||||||||||||||||
24.In covering a certain distance, the speeds of A and B are in the ratio of 3 : 4. A takes 30 minutes more than B to reach the destination. The time taken by A to reach the destination is:
Sol:
| ||||||||||||||||
Ratio of speeds = 3 : 4. Ratio of times taken = 4 : 3.
| ||||||||||||||||
Suppose A takes 4x hrs and B takes 3x hrs to reach the destination. Then,
| ||||||||||||||||
| ||||||||||||||||
|
25.A person has to cover a distance of 6 km in 45 minutes. If he covers one-half of the distance in two-thirds of the total time, to cover the remaining distance in the remaining time, his speed (in km/hr) must be:
Sol:
| ||||||||||||||
| ||||||||||||||
|
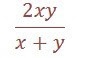





No comments:
Post a Comment